Matematiksel Özellikleri
Beklenen değerleri μX ve μY, standart sapmaları σX ve σY olan iki bağımsız değişken X ve Y arasındaki korelasyon katsayısı (ρX, Y), şu şekilde tanımlanır:
E değişkenin beklenen değerini, cov ise kovaryansı ifade eder,
μX = E(X) olduğundan, σX2 = E(X2) − E2(X) ve
Y, için de aynısı geçerli olduğundan, şu ifadeyi yazabiliriz:
Korelasyon, yalnızca standart hataların ikisi de sonlu ve sıfırdan farklı ise tanımlıdır. Korelasyon katsayısının 1'i (mutlak değer olarak) geçemeyeceği ise Cauchy-Schwarz eşitliğinin doğal bir sonucudur.
Tam bir artan doğrusal ilişkinin varlığı halinde korelasyon katsayısı 1 değerini alır, tam bir azalan ilişkinin varlığı halinde ise korelasyon katsayısı -1 değerini alır. Katsayının alabileceği diğer tüm değerler ise ilişkinin doğrusallığına bağlı olarak bu iki değer arasında olacaktır. Katsayı 1'e veya -1'e ne kadar yakınsa ilişkinin doğrusallığı o kadar güçlüdür.
Değişkenler istatistiksel olarak bağımsız ise korelasyon 0'dır fakat bunun tersi doğru değildir, çünkü korelasyon katsayısı yalnızca doğrusal olan ilişkiyi belirler.
Bir örnek: TesadüfiX değişkeninin −1 ve 1 aralığında tekdüze dağıldığını varsayalım ve Y = X2 ilişkisi geçerli olsun. Bu durumda Y tamamen X tarafından belirlenmiştir, öyle ki X ve Y birbirlerine bağımlıdır, fakat Pearson anlamdaki korelasyon 0 olacaktır. Ne var ki, X ve Y'nin birlikte normal dağıldığı durumda, istatistiksel bağımsızlık aynı zamanda korelasyonun da olmaması anlamına gelir.
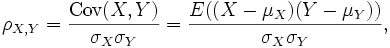

Hiç yorum yok:
Yorum Gönder